It appears that if you sum along the diagonal’s of Pascal’s triangle, it follow’s the Fibonacci sequence. Pascal’s triangle is often used to find the coefficients of a binomial $(x+y)^{n}$. This can also be expressed with combinatorics, which is written on the side of each bubble in the triangle.

For this post we will assume that $F_{0}=1$, $F_{1}=1$ and the Fibonacci sequence is generated by $F_{n}=F_{n-1}+F_{n-2}$.

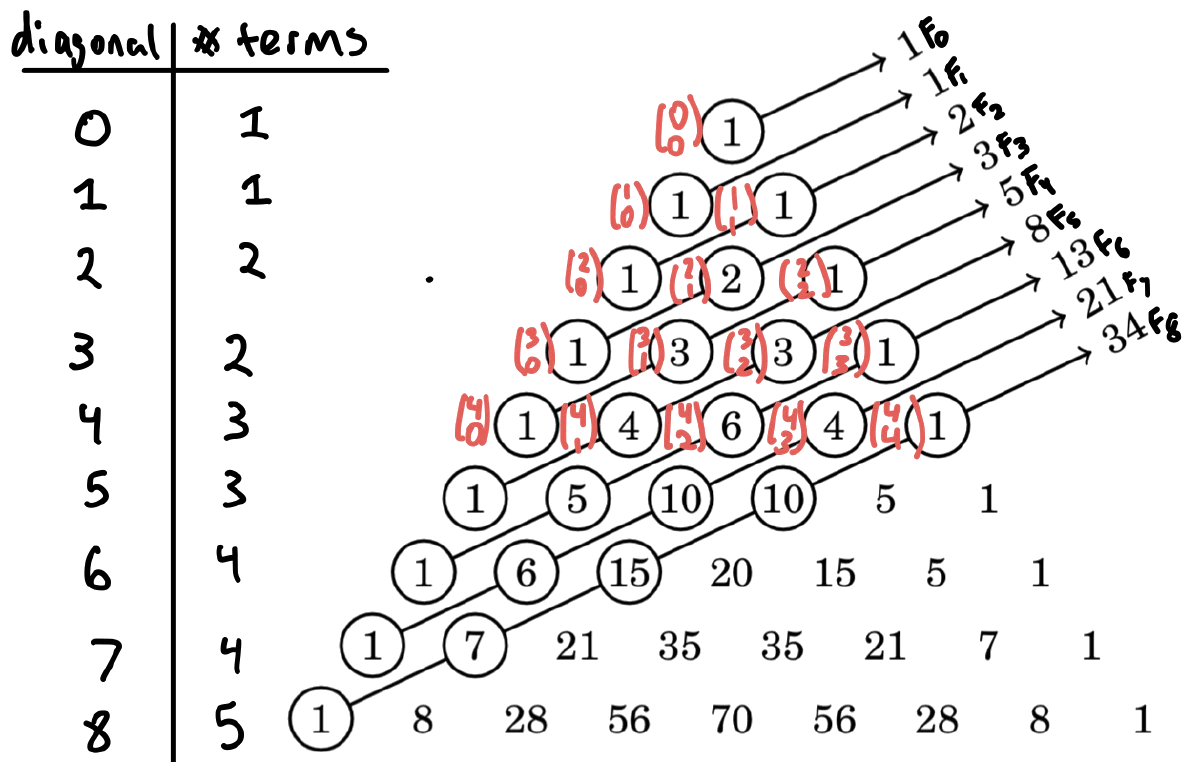
To demonstrate this using combinatorics, the 4th (5th if you don’t count from 0) diagonal’s sum looks like $$ {4 \choose 0} + {3 \choose 1} + {2 \choose 2} =1+3+1 = 5 $$ Which is equal to $F_{4}$ .

We can extrapolate and guess that the pattern continues along the lines of $F_{n} =\sum_{k=0}{n -k \choose k }$. The top term, $n-k$, decreases as k increase, while the bottom number $k$ increases with the sum.

However the number of terms in a diagonal depends on the particular Fibonacci number you are evaluating. If you look at the table in the photo, the number of terms in a diagonal follows a floor pattern. The expression is exactly $\lfloor \frac{n}{2}+1 \rfloor$

We will prove with strong induction that the n-th Fibonacci number is equal to $$F_{n}=\sum_{k=0}^{\lfloor \frac{n}{2} +1\rfloor } {n-k \choose k}$$

Proof

Base case

When $n=0$, $F_{0}=1$ and $$\sum_{k=0}^{\lfloor 0+1 \rfloor}{0-k \choose k}={0-0 \choose 0}+{0-1 \choose 0}=1+0=1$$ $F_0$ and the sum are equal.

When $n=1$, $F_{1}=1$ and $$\sum_{k=0}^{\lfloor \frac{1}{2}+1 \rfloor}{1-k \choose k }={1-0 \choose 0}+{1-1 \choose 1}=1+0=1$$ $F_1$ and the sum are equal.

Therefore, the base case holds.

Inductive step

Assume that for $j\in\mathbb{N}$ and $j\geq 1$ we know how to construct the k-th Fibonacci number as long as it is in the interval $0 \leq k \leq j$ (the interval our base cases are in).

Consider the $j+1$ Fibonacci number. We will proceed with a proof by cases, when $j$ is even and when $j$ is odd.

Case 1: $j$ is even.

Because $j$ is even, it is a multiple of two. So $j=2m$, $m \in \mathbb{Z}$. Then we know that $$F_{j}=\sum_{k=0}^{\lfloor \frac{2m}{2}+1 \rfloor} {j-k \choose k} \text{ and }F_{j-1}=\sum_{k=0}^{\lfloor \frac{2m-1}{2}+1 \rfloor} {j-k \choose k}$$ We can simplify the upper bounds of each sum.

$$\lfloor \frac{j}{2}+1 \rfloor=\lfloor \frac{2m}{2}+1 \rfloor=\lfloor m+1 \rfloor=m+1$$ $$\lfloor \frac{j-1}{2}+1 \rfloor=\lfloor \frac{2m-1}{2}+1 \rfloor=\lfloor m+\frac{1}{2} \rfloor=m$$

Therefore $F_{j}=\sum_{k=0}^{m+1}{2m-k \choose k}$ and $F_{j-1}=\sum_{k=0}^{m}{2m-1-k \choose k}$

Continuing with the proof, we will make use of the fact that ${{n \choose k-1}+{n \choose k}={n+1 \choose k}}$ (See proof)

$$ \begin{aligned} F_{j+1}&=\sum_{k=0}^{m+1}{(2m+1)-k \choose k} = \sum_{k=0}^{m+1}{2m-k \choose k}+\sum_{k=0}^{m+1}{2m-k \choose k-1} \\ &=F_{j}+\sum_{k=0}^{m+1}{2m-k \choose k-1} \\ &=F_{j}+\cancel{2m-0 \choose 0-1}+\sum_{k=1}^{m+1}{2m-k \choose k-1} \end{aligned} $$ We evaluate the first term of the sum. This ends up being 0 because you can’t choose a negative number of elements (0 ways to do so) ${2m-0 \choose 0-1}={2m \choose -1}=0$

Next we re-index the sum. Let $u=k-1$, then $$ \begin{aligned} F_{j+1}&=F_{j}+\sum_{u=0}^{m}{2m-(u+1) \choose u} \\ &=F_{j}+\sum_{u=0}^{m}{2m-1-u \choose u} \\ &=F_{j}+F_{j-1} \end{aligned} $$

Case 2: $j$ is odd.

Because $j$ is odd, then it can be written as a multiple of 2 plus one. So ${j=2m+1}$ where $m \in\mathbb{Z}$.

To streamline our work, let us simplify the floor evaluations. $$ \begin{aligned} j:&\lfloor \frac{j}{2}+1 \rfloor=\lfloor \frac{2m+1}{2}+1 \rfloor=\lfloor m+\frac{3}{2} \rfloor=m+1 \\ j+1:&\lfloor \frac{j+1}{2} +1 \rfloor = \lfloor \frac{2m+1+1}{2}+1 \rfloor=\lfloor m+2 \rfloor=m+2 \\ j-1:&\lfloor \frac{j-1}{2}+1 \rfloor = \lfloor \frac{2m+1-1}{2}+1 \rfloor=\lfloor m+1 \rfloor=m+1 \end{aligned} $$

Then $F_{j}=\sum_{k=0}^{m+1}{(2m+1)-k \choose k}$ and $F_{j-1}=\sum_{k=0}^{m+1}{2m-k \choose k}$.

Continuing with the proof and making use of the same identity as before: $$ \begin{aligned} F_{j+1}&=\sum_{k=0}^{m+2}{(2m+1)+1-k \choose k } = \sum_{k=0}^{m+2}{(2m+1-k)+1 \choose k } \\ &=\sum_{k=0}^{m+2}{2m+1-k \choose k}+\sum_{k=0}^{m+2}{2m+1-k \choose k-1} \end{aligned} $$

We evaluate the last term of the first sum. Then we evaluate the first term of the second sum. $$ \begin{aligned} F_{j+1}&={2m+1 - (m+2) \choose m+2 } +\sum_{k=0}^{m+1}{2m+1-k \choose k}+{2m+1-0 \choose 0-1}+\sum_{k=1}^{m+2}{2m+1-k \choose k-1} \\ &=\cancel{m-1 \choose m+2 } +F_{j}+ \cancel{2m+1 \choose -1}+\sum_{k=1}^{m+2}{2m+1-k \choose k-1} \end{aligned} $$ Re-index the second sum. Let $u=k-1$. $$ \begin{aligned} F_{j+1}&=F_{j}+\sum_{u=0}^{m+1}{2m+1-(u+1) \choose u} \\ &= F_{j}+\sum_{u=0}^{m+1}{2m-u \choose u}=F_{j}+F_{j-1} \end{aligned} $$

$\therefore$ Therefore, we have shown using strong induction that the sum along the diagonals of Pascal’s triangle follow’s the Fibonacci sequence.